The algorithm for finding love
Hinge, matchmaking, and two mathematicians you may have to thank for landing that first date.
I wrote quite a few of my favorite articles before ever sharing my thoughts with folks, so as February aka Valentine’s month, has come to an end, I’m bringing back one of my favorite past posts about one of the most lovable use cases for data out there - dating. No AI - just good, ole-fashioned, algorithmic matchmaking. Enjoy!
I took my first algorithms class during my junior year and learned of an algorithm that has since become one of my favorite pieces of knowledge acquired during college. This algorithm has a beautiful story, including a Nobel Prize, medical residents, and the dating app, Hinge. This algorithm is known by the name of its two creators, Gale-Shapley, and I just love it.
Today, we’ll explain the algorithm and walk through how it applies to a feature on one of the world’s most popular dating apps that you may have a love hate relationship with - Hinge’s Most Compatible.
Some background to get started
David Gale and Lloyd Shapley were mathematicians and economists. They both found success tackling problems in game theory, logic, and eventually received the Nobel Prize in Economic Sciences in 2012 for their work, citing the success of a 1962 paper titled “College Admissions and the Stability of Marriage”.
Their paper proposed a problem you’ve probably thought about if you’ve applied to college: “A college is considering a set of n applicants of which is can admit a quote of only q. Having evaluated their qualifications, the admissions office must decide which ones to admit.” There is a desire from both applicant and college that assigning applicants to the right college be satisfactory for both student and college - the student goes where they want and the college gets the students they’d like. This algorithm hopes to tackle finding those most desired matches for all participants.
How does the algorithm work?
While they ultimately wanted to provide a solution to the college admissions problem, having far more applicants than colleges can make it harder to tackle than a problem in which there is equal numbers in each sets of the problem. We’ll simplify things by assuming these are equal.
We have n colleges and n applicants.
Each set ranks the members of the other set by their preference - ie. all colleges rank the applicants from most desired to least desired and the applicants rank the colleges as well.
The goal is finding a stable set of matches, with stable as being not unstable. A match is unstable if there are two applicants X and Y who are assigned to colleges A and B, respectively, although Y prefers A to B and A prefers Y to X.
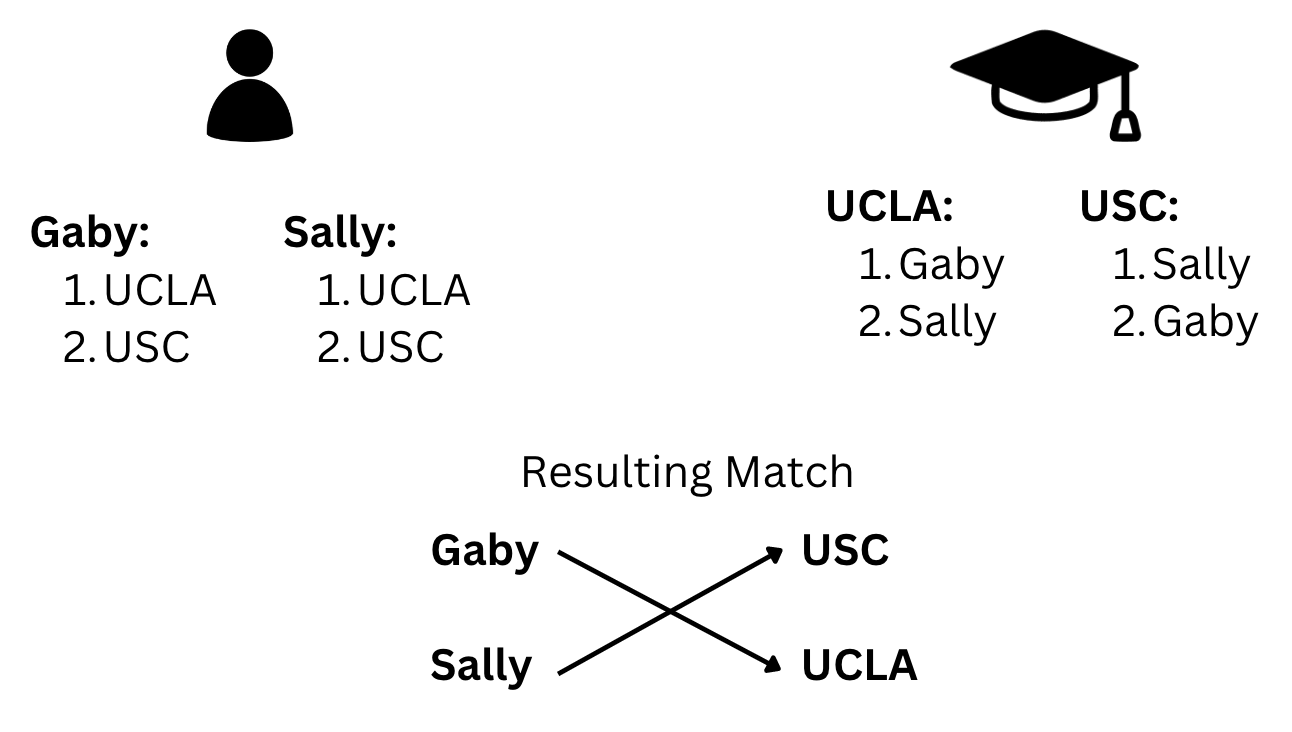
To explain this in real life, imagine there are two students, Gaby and Sally. They are deciding where they’d like to go to college. They both rank the only two colleges that exist, USC and UCLA, by their preference. The two colleges rank Gaby and Sally.
Let’s look at these lists.
Take a look at how Sally and Gaby have the same lists. While Sally preferred UCLA over USC, a match of Sally at UCLA would have been unstable, since UCLA preferred Gaby over Sally and Gaby preferred UCLA over USC, which is a stable match.
Gale and Shapley’s paper proves that there always exists a stable set of matches (marriages in the case of the stable marriage problem). These matches are revealed through iterations of the Gale Shapley algorithm. For a technical walkthrough of the algorithm, check out the matching python package docs on the problem.
Taking from Gale and Shapley’s paper, which defined the algorithm to begin with, let’s explain how it technically works in the scope of marriage, despite the antiquated view.
Each man proposes to his most preferred woman.
Each girl who receives more than one proposal rejects all but her most preferred. She does not accept this most preferred, but says “maybe” for now.
The second round begins. The rejected men each propose to their second most preferred woman. The women receiving a proposal choose their favorite man from the new proposals she has received and her “maybe” match from the first round, if she had one.
This proceeds again, with more proposals and the women rejecting all but the best proposal they have received so far.
The proposals continue until the last woman gets proposed to and all the women must accept whoever she has most recently preferred the most.
It’s import to make note that the execution of the stable marriage problem in this way is optimal for the men. One could conduct the same experiment with the women proposing, and if the match from that experiment was the same as the match from the male proposing experiment, that match would be considered optimal.
Other versions of the algorithm include:
The stable roommates problem where there is only one set of individuals, not two
The hospital-residents problem which uses a variation of the algorithm to match medical school graduates with residency programs, and a further variation for couples who are allowed to be considered when preferring to stay together for residency
Where is the algorithm used today?
You’re scrolling through Hinge, liking, messaging, and denying potential matches on your quest to find love. You’re getting closer and closer to that special someone. All those interactions are generating data for Hinge to establish your preferences. While you never explicitly draft up a list ranking every single person in your dating pool, your likes, messages, We’ve Mets, and more all indicate the type of individual you are looking for.
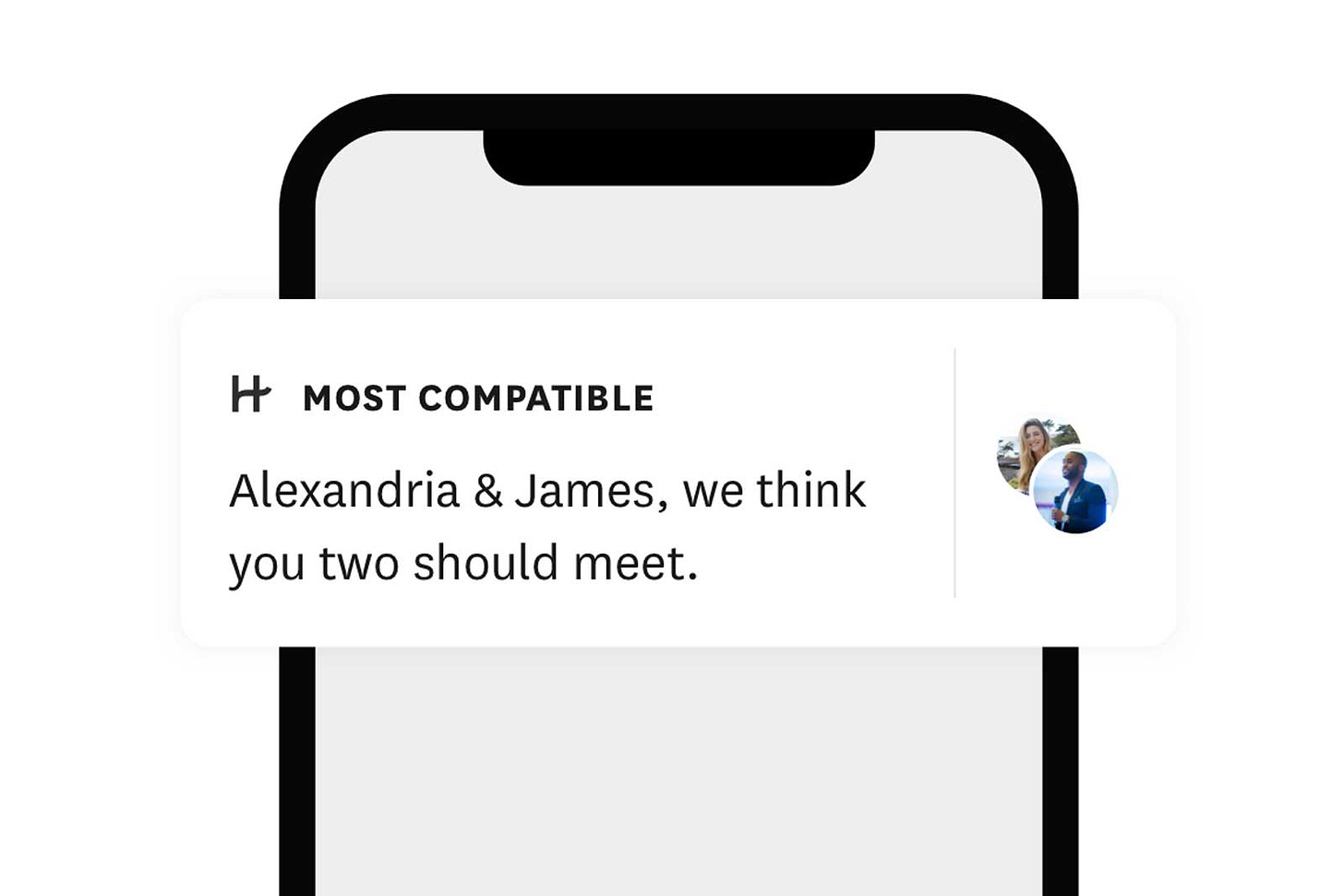
Hinge’s Most Compatible feature ”uses machine learning to figure out each user’s taste” according to CEO Justin McLeod. The app is aggregating data on your actions to develop a personalized view of what you’re looking for while also aggregating views for those in your dating pool. The models are then applying a variation of the stable marriage problem to promote those who you are Most Compatible with. Both users in a Most Compatible match receive the notification on the same day and it expires after 24 hours. The process continues to repeat and hopefully be more and more successful with continued use of the app. Users have said that the app’s recommendations improve the more time you spend on the app, and that is due to the app’s ability to better understand your preferences with an increased number of likes, dislikes, messages and more.
Data science and a variation of the Gale-Shapley algorithm is powering the recommendations you receive every day on Hinge. It’s iterating every day, with more training data and improved understanding of users, to help you get one step closer to finding your Most Compatible.
A fun tidbit to end today’s post: Did you know Hinge CEO Justin McLeod’s own love story has made it to TV? What started off as a conversation with a New York Times journalist evolved into Justin reaching back out to “the one that got away” after being inspired by his conversation. The interview and love saga was turned into an episode of Amazon Prime’s Modern Love which is inspired by the NYT article series.
So it turns out data science is helping out millions in their journey to find love, hoping to better understand our preferences, ideal partners, and eventually find the perfect match. Thanks for reading this week’s post.